
Therefore, we can decrease the probability of Type II errors by Usually, power is an increasing function of sample size: the more observations If a test has high power, then there is a low probability of If a test has low power, then there is a high probability of If we denote the probability of committing a Type II error by

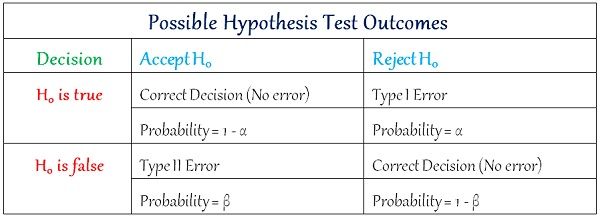
The power of a test is the probability that the test will reject a false null The function that links the value of the true variance to the probability of a Pinned down, but it depends on the true variance. Therefore, the probability of committing a Type II error is not uniquely However, it depends on the true and unknown variance Probability can be calculated using the distribution function of a In this example, the probability of committing Type II errors is This is a Type II error! We are not rejecting the null even if it is false. Then we fail to reject the null hypothesis Then we do not reject the null hypothesis The outcome of the hypothesis test is determined as follows: We check whether the value taken by the Chi-square statistic belongs to a Variance, we can use the Chi-square statistic as a test statistic. We want to test the null hypothesis that the variance of the distribution is Suppose that we observe a sample of draws We will explain below that the probability of committing Type II errors can beĮxactly quantified through a function called Random variable (the test statistic) will not belong to the critical region. Type II error occurs is equal to the probability that the Thus, before the data is observed, the test statistic In turn, this value depends on the data usedīut the data is random. This decision process is prone to the following kind of error: we mayįail to reject the null hypothesis when it is false.Įrrors of this kind are dubbed Type II errors, in order to distinguish themįrom Type I errors, which occur when the null hypothesis is rejected despiteĮarlier we mentioned that the outcome of a test of hypothesis depends on the We reject the null hypothesis when the value taken by the statistic belongs toĪ critical region that has been specified in advance Should be rejected or not, based on a test When we perform a test of hypothesis, we decide whether the null hypothesis

Type II errors are also referred to as errors of the second How to reduce the probability of Type II errors


 0 kommentar(er)
0 kommentar(er)
